Table of Contents
What is Returns to Scale?
The changes in total output on account of the change in the factors of production in the same proportion is called the returns to scale. In the long run, all the factors of production are variable and even the scale of production can be changed according to the demand for various goods and services in the economy.
Returns to Scale
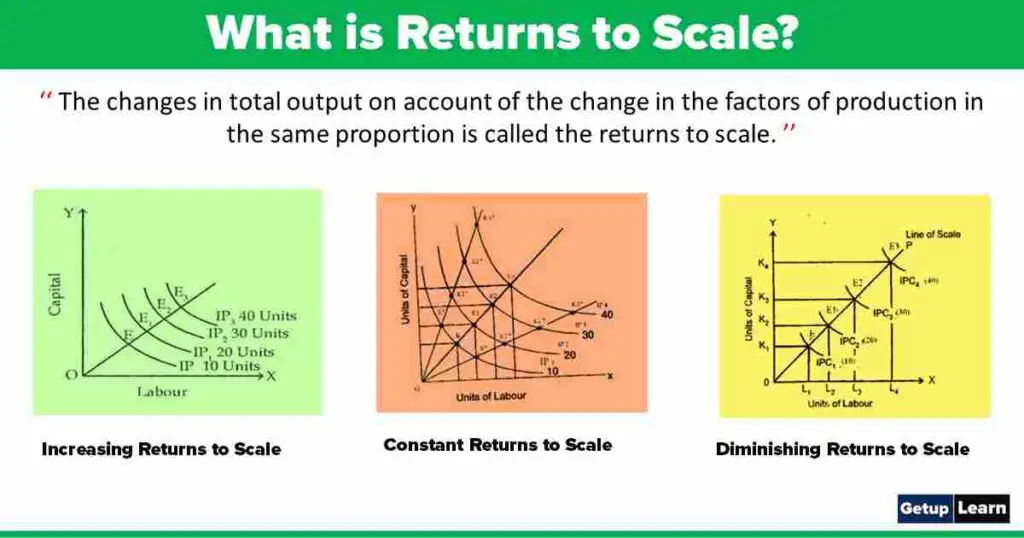
Returns to scale are concerned with a long term production function. It is studied with the help of iso-product curves. Returns to scale are of three types as shown below:
Increasing Returns to Scale
When the change in total output is more than in proportion to the proportional change in all the factors of production then it is called the increasing returns to scale. Thus the rate of increase in output is higher than the increase in factors of production.
When the distance between various iso product curves decreases on the expansion path or scale line then the increasing returns to scale will operate. It reveals that the increase in output in the same proportion requires less ratio of labour and capital.
Thus output increases more than in proportion to the units of factors of production employed under this law. It can be explained with the help of the following diagram:
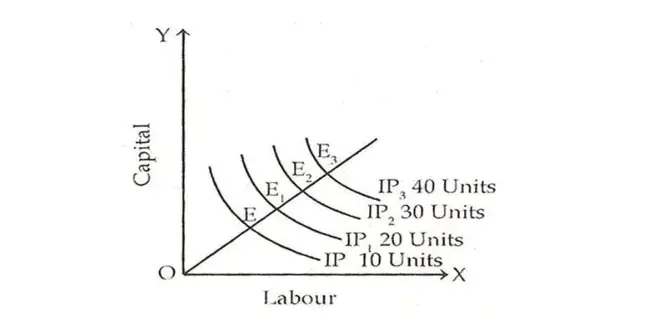
Capital and labour are shown on oy-axis and ox- axis respectively. IP, lP1, 1P2 and lP3 are different iso-product curves showing different levels of output viz 10 units, 20 units, 30 units and 40 units. The distance between successive iso-product curves diminishes as output is expanded by increasing the scale. The distance OE> EE1> E1E2>E2E3 which reveals that for equal increase in output, firm has to employ less and less amount of labour and capital.
Causes of Operating the Law
The increasing returns to scale operates on account of the following causes or reasons:
- Indivisibilities of Inputs
- Division of Labour and Specialisation
- Dimensional Efficiency
- Economies of Large Scale
Indivisibilities of Inputs
There are some factors of production which are indivisible. Indivisibility means that they are available in a given shape or can not be divided into small pieces. Machine, managers, research, finance and marketing are such examples of individualities. With the increase in the scale of production, the efficiency increases and the output increases more than in proportion to the change in inputs.
Division of Labour and Specialisation
When the scale of production has increased the division of labour and specialisation is introduced. A process of production is divided into sub-process and each process is completed by each group of workers and at the same time, the specialist is appointed for different departments viz finance manager, marketing manager, personnel manager, purchasing manager and so on. Their services lead to an increase in production and increasing returns to scale operations.
Dimensional Efficiency
Increasing returns to scale is the result of operating dimensional efficiency in a business firm that is on account of the large size. The size increases the efficiency of all inputs and the increasing returns operate. Thus the investment in capital assets after a point will increase the output due to increased dimension of efficiency.
Economies of Large Scale
When the scale of production is increased the internal and external economies of scale will operate and on account of it, the increasing returns to scale will also operate. Internal economies are on account of firms own size and organisation while external economies are caused by the concentration and localisation of industries. All these economies lead to an increase in output more than in proportion to the change in the ratio of two inputs.
Constant Returns to Scale
When the total output of a firm increases in the same proportion in which the change in inputs takes place the law is called constant returns to scale. The proportion of two inputs remains constant.
When all iso-product curves showing the same level of output have an equal distance between them on the expansion path or scale line, the law operating is called constant returns to scale. It is explained with the diagram.
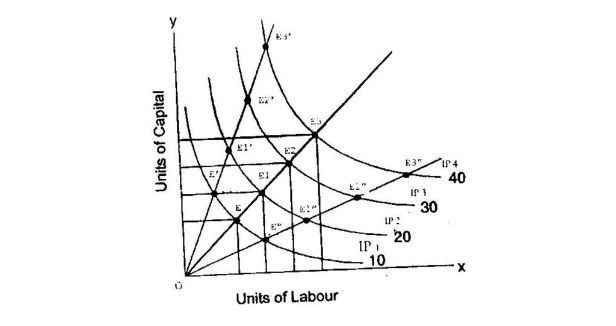
Capital and labour are shown on oy-axis and ox-axis respectively IP, IP1, IP2 and IP3 are different in product curves showing different levels of output viz 10 units, 20 units, 30 units and 40 units. The distance between iso-product curves is indicated by E, El, E2 and E3.
The distance on the scale line (OP) are equal. OE = EE1 = E1E2 = E2E3. The distance between all iso- product curves remains constant, which reveal that the production increases in the same proportion in which inputs are changed. Hence it is constant returns to scale.
This law operates at the point where neither the internal and external economies nor internal and external diseconomies are enjoyed by the firm during the long period.
Diminishing Returns to Scale
When proportionate change total output is less than the proportionate change in all the factors of production then, the diminishing returns to scale will operate.
The distance between various iso-Product curves on the scale line increases, the diminishing returns to scale will operate Because for getting the same level of output we have to employ more of all inputs. It is explained with the help of the following diagram:
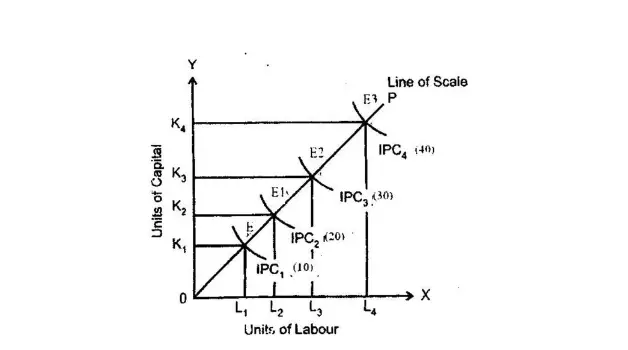
Labour and capital are employed on ox-axis and oy-axis. OP is the scale line on which E, El, E2 and E3 different is product curves are showing different levels of output. The distance between these curves is increasing on the scale line which shows that we have to employ more inputs and the resultant output is less than in proportion to the change in inputs. OE<EE1<E1 E2<E2E3 which show the diminishing returns to scale.
Causes of Operating the Law Diminishing Returns to Scale
The diminishing returns to scale operate on account of the following reasons:
- Diseconomies of Large Scale
- Delay in Decision-making and Its Implementation
- Managerial Inefficiency
- Entrepreneur is Not Variable
Diseconomies of Large Scale
When the scale of production is increased, the internal and external diseconomies of scale operate. On account of these diseconomies, the output increases less than in proportion to the change in the inputs and the diminishing returns to scale operates.
Delay in Decision-making and Its Implementation
With the size of the scale of production, the decisions are taken at different levels of management. Delay in decision-making and its implementation lead to an increase in output less than in proportion to the change in all variable inputs. Pressure from top management, red-tapism and diseconomies of managerial skill lead to diminishing returns to scale.
Managerial Inefficiency
With the increase in the size and scale of production in the long period the management becomes a complicated process. It results in managerial inefficiency leading to the operation of diminishing returns to scale operations.
Entrepreneur is Not Variable
An entrepreneur is one of the factors of production. He is neither variable nor divisible input. In practice, he is fixed and indivisible input and on account of change in other variable inputs the ratio under the large scale leads to imbalances and the law of diminishing returns to scale operates.
What is return to scale with example?
Production function is the functional relationship between input and output. It is divided into two parts i.e. short run production function and long run production function. Short run production function is applicable in short period. Short period is that period in which at least one factor remains fixed and at least one factor remains variable. It is known as law of returns.
How can you explain law of Return to scale?
The changes in total output on account of the change in the factors of production in the same proportion is called the returns to scale. In the long run all the factors of production are variable and even the scale of production can be changed according to the demand for various goods and services in the economy. Returns to scale is concerned with long term production function. It is studied with the help of iso-product curves. Returns to scale are of three types (1) Increasing returns to scale, (2) Constant Returns to Scale, (3) Diminishing Returns to Scale.